Test examples of boundary value problems: second order scalar cases

1 Example1

This is a linear case satisfying strong uniqueness and smoothness conditions. The problem is

y " = \frac{2 y}{(1 + x)^{2}}, y (0) = 1, y (1) = \frac{1}{2}

with the unique and arbitrarily smooth solution

y (x) = \frac{1}{1 + x} .

This case satisfies all properties of the basic theorem and hence the theoretical properties can be verified perfectly here. Because of this and the linearity in

y

Newton's method finds the true solution in one step, but in order to detect this it takes a second one.

2 Example2

This is a nonlinear, uniquely solvable, but sensitive case. Simple shooting gets trouble here if the initial slope is not near the true value

9 / 20

, since the singularity moves into

] 0, 1 [

for a guess of the initial slope greater than 1/2.

y " = (y')^{2}, y (- 1) = 0, y (1) = \log (10)

with the unique and arbitrarily smooth solution

y (x) = - \log (\frac{11}{20} - \frac{9}{20} x)

Observe that there occurs an essential singularity at

x = 11 / 9 = 1.222 \dots

and that hence the truncation error is a bit larger than in example one. Due to the nonlinearity Newton's method needs a bit more work, but there is no essential problem if one starts not too far from the true solution. But observe that the condition of global boundedness of

\frac{\partial f}{\partial y'}

is not satisfied here. Again Richardson extrapolation works well.

3 Example3

This is a nonlinear nonuniquely solvable case with two smooth solutions.

y " = - \exp (y + 1), y (0) = 0, y (1) = 0 .

It has two solutions

y (x) = - 2 \log (\frac{\cosh ((x - \frac{1}{2}) \frac{θ}{2})}{\cosh (\frac{θ}{4})})

where

θ

is one of the two solutions of

θ = \sqrt{2 e} \cosh (\frac{θ}{4}) .

These values are

θ = 3.036231848196573

for the lower and

θ = 7.135005531636586

for the upper solution.

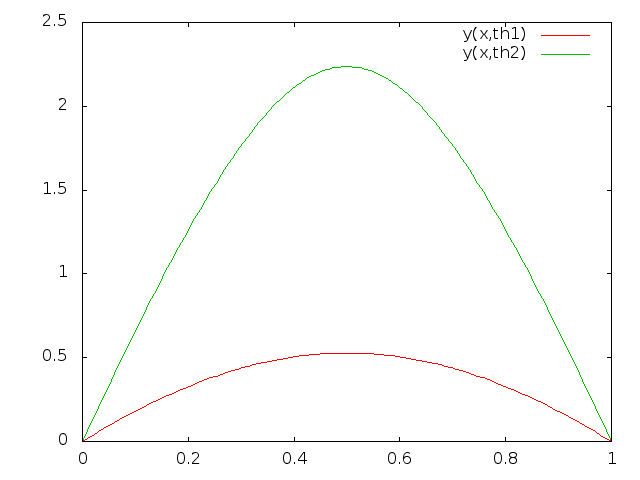Both solutions are very smooth and anything works well, also Newton's method has no trouble.

4 Example4

This again is a second order problem which exhibits the possibility of a nonunique solvability of an otherwise well behaved boundary value problem. The ode is

y " = \frac{3}{2} y^{2} .

With the Dirichlet boundary conditions

y (0) = 4, y (1) = 1

the problem has two solutions. The first one is

y (x) = \frac{4}{(x + 1)^{2}}

the other can be expressed with higher transcendental functions only. We select the one above by prescribing different , so called Robin boundary conditions

\begin{matrix} 2 y (0) + y' (0) & = & 0 \\ 3 y (1) + y' (1) & = & 2 . \end{matrix}

This example allows to study the effects of first and second order approximations of the boundary derivatives. If discretized with the right resp left first order difference quotient the truncation error shows up odd terms in

h

and hence Richardson extrapolation as done here has no essential effect. But since the differential equation and its solution can be safely extended outside

[0, 1]

we can use the technique of fictitious nodes

a - h

and

b + h

which in turn allow for the symmetric second order difference quotient. In this case the truncation error has an expansion in even powers of

h

only and the extrapolation works well.

5 Example 5

Here we study the effects of a differential equation which is defined inside

] 0, 1 [

only.

y " = \frac{12 y}{x^{2}} + 7 x^{2} for 0 < x < 1 .

With the boundary conditions

y (0) = y (1) = 0

the solution becomes

y (x) = x^{4} \ln (x) .

Clearly the use of fictitious points is impossible here. Since we have Dirichlet boundary conditions only the truncation error for

y " (x_{i})

, which is

\frac{1}{12} y^{(4)} (x_{i}) h^{2} + \frac{1}{360} y^{(6)} (ξ_{i}) h^{4} with ξ_{i} \in] x_{i - 1}, x_{i + 1} [

plays a role. But

y^{(4)} (x) = 24 \ln (x) + 40

hence for

x_{i}

near the left boundary the truncation error will be quite large and we will get considerable trouble here and Richardson extrapolation shows no much effect.

6 Remark

If the boundary singularity becomes stronger, e.g. for

y " = \frac{3 x}{y}, y (0) = 0, y' (1) = 3

with the solution

y (x) = 2 x^{3 / 2}

the situation becomes hopeless.

7 Example 6

This is a linear problem with homogeneous Dirichlet boundary conditions.

y " = 60 y' - 60, y (0) = 0, y (1) = 0

with the solution

y (x) = x - \frac{\exp (60 x) - 1}{\exp (60) - 1} .

It shows a strong instability, hence shooting would get considerable trouble. Here this trouble comes in as a restriction on the gridsize

h

File translated from T_EX by T_TM Unregistered, version 4.03.
On 20 Jun 2016, 18:02.