Initial value problems: predefined cases

• onedimensional model equation y'(t) = -2y(t) with initial value y(0) = 1. Analytical solution is y(t) = e^-2t. Endpoint of integration is b = 1. This is an easy case, where even Euler will perform well.

• onedimensional case with a moving singularity y'(t) = y² with initial value y(0) = 0.25. Solution is y(t) = 1/(4-t). Here b is chosen shortly before the singularity: b= 3.95 at t = 4. Hence you should observe near b a strong reduction of the stepsize and a sharp growth of the global error.

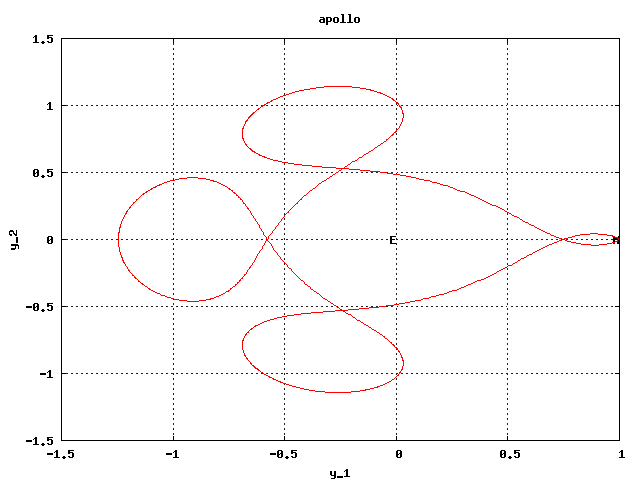
• The restricted three body problem (has a common plane) (earth - moon - Apollo module). written as a first order system it has 4 components which read
  1. F₁(t,y) = y₂.
  2. F₂(t,y) = y₁ + 2y₄(t) -ν (y₁ + μ) / SQRT[ ((y₁ + μ)² + y₃²)³ ] - μ (y₁ - ν) / SQRT[ ((y₁ - ν)² +y₃²)³ ].
  3. F₃(t,y) = y₄.
  4. F₄(t,y) = y₃ - 2 y² - ν y₃ / SQRT[ ((y₁ + μ)² + y₃²)³ ] - μ y₃ / SQRT[ ((y₁ - ν)² +y₃²)³ ].
  Initial values are y(a = 0) = (0.994, 0, 0, -2.00158510637908252)^T leading to a periodic orbit of APOLLO. Integration begins at the back side of moon. Smallest deviations in the initial values resp. discretization errors destroy the periodicity and lead finally to enormous deviations from the intended path. Because of the period length of b=17.0652165601579625 the global discretization error there is the deviation of the final values from the initial values and one can check the correctness of the global error estimation. You might play with tol and smally in order to realize this. smally must be small indeed, otherwise you will get senseless results. The system is not stiff however. The coordinate system moves together with moon around the earth, with x-axis = moon-earth connection, earth center at μ = -0.012277471 and moon center at ν = 1-0.01227747, y(1) and y(3) are the coordinates of the Apollo modul in this coordinate system and y(2), y(4) is the speed vector.
  

• The nonlinear RLC circuit with a tunnel diode in parallel position receives voltage from an external source which is taken from a periodic jump function, (+/-0.022). The current in this circuit is periodic in the limit. The system is very stiff and the solution oscillates in [0,1] very strongly. Initial time is a = 0 and endtime b = 16. Problems occur, if the stepsize has the order of magnitude of the period of the external source.
  
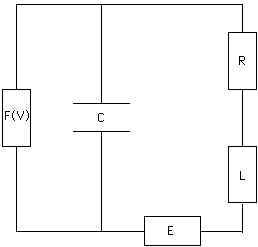
  The data of this circuit are L = 0.01, C = 0.01 , E = E0 + S(t)DE, DE=0.022 , S(t) = +/- 1 , R=0.017 F(V)= 6650*V*(V**2- 3*(0.148*V - 0.0167) )

• The reduced Reynolds equation describes in a quite simplified form the motion of a metallic ring pressed down in a viscous fluid towards a fixed plate with force p(t). This equation is strongly nonlinear and extremely stiff.
  
  1. F₁(t,y) = -(c1*c3*c4*c5**3/c2)*y₁/(y₂³) -p(t)/c2,
  2. F₁(t,y) = y₁ .
     
  This stiffness increases with time. The component y(2) > 0 is the distance from the plate going to zero and y(1) is velocity. The integration interval is [0,2].

• A scalar equation with discontinuous right hand side (jump discontinuity of F, with a kink in the true solution).

  F(y,t) = y(t)², if 0<= t <= 1/sqrt(2) and
  F(y,t) = 2(y(t)-y(1/sqrt(2))-1), if t > 1/sqrt(2).

  Initial value is y(0) = 1 and integration ends at b = 3. You should observe a sharp reduction in the stepsize at t=0.707... and a strong jump in the local discretization error, which in turn yields an unrecoverable growth in the global error.

back to the theory page